Matrix: Python version!

Matrix: Python version! 🐍

“What is the Matrix? It is the world that has been pulled over your eyes to blind you from the truth.” - Morpheus, The Matrix (1999)

Introduction to Matrices ⚔️

What is Matrix?

Is it like The Keanu Reeves movie, "The Matrix"? Where he comes in a black suit and black glasses? Stopping all the bullets? 😵

Keanu Reeves (as Neo) stopping bullets 🗿

NO! Right? Its not like the movie…

Well, In mathematics, a matrix is a two-dimensional array of numbers, symbols, or expressions arranged in rows and columns. It holds significance across diverse fields like computer graphics, physics, machine learning, and more.

Same in Python!

Creating a Matrix in Python

Let’s create a simple 3x3 (3 rows, 3 columns) matrix using Python’s built-in lists:

# Creating a 2x3 matrix
matrix = [
  [1, 2, 3], # first row
  [4, 5, 6]  # second row
  [7, 8, 9]  # third row
]
print("Matrix: ")
for row in matrix:
    print(row)

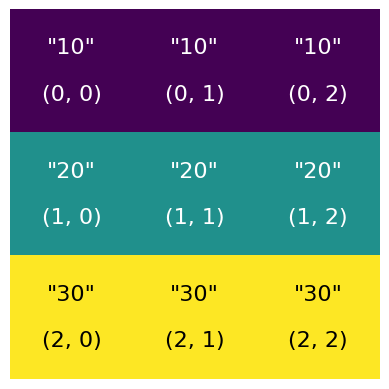
This image shows a 3x3 matrix, with the corresponding row position and column position.

That’s it! 🎉 Congratulations! You just created a matrix in Python.

Well… We are going good so far. Let’s see if we can make it more interesting 🎉

Matrix Operations

We can use various matrix operations in Python. For example, we can add two matrices together:

Let’s start with some simple examples:

Addition

# Define matrices
matrix1 = [[1, 2, 3],
           [4, 5, 6],
           [7, 8, 9]]

matrix2 = [[9, 8, 7],
           [6, 5, 4],
           [3, 2, 1]]

# Initialize a result matrix with zeros of the same size
result = [[0, 0, 0],
          [0, 0, 0],
          [0, 0, 0]]

# Perform matrix addition
for i in range(len(matrix1)):
    for j in range(len(matrix1[0])):
        result[i][j] = matrix1[i][j] + matrix2[i][j]

# Displaying the result
print("Matrix Addition Result:")
for row in result:
    print(row)

Wait wait wait…, do not panic that we are using nested for loops. (we have to 💀)

But Don't worry, I'll explain everything in detail !

• matrix1 and matrix2 are two matrices defined using nested lists.
• result is initialized as a matrix filled with zeros of the same size as matrix1 and matrix2.
• On line number 16 and 17, for loops are used to iterate over the rows and columns of matrix1 and matrix2.
• On line number 18, result[i][j] is used to store the sum of the elements in matrix1[i][j] and matrix2[i][j].
• Well, you know the print part.

Cool, we are done! 🎉 Let’s see what else we can do with matrices!

Multiplication

# Define matrices
matrix1 = [[1, 2],
           [3, 4]]

matrix2 = [[5, 6],
           [7, 8]]

# Initialize a result matrix with zeros
result = [[0, 0],
          [0, 0]]

# Perform matrix multiplication
for i in range(len(matrix1)):
    for j in range(len(matrix2[0])):
        for k in range(len(matrix2)):
            result[i][j] += matrix1[i][k] * matrix2[k][j]

# Displaying the result
print("Matrix Multiplication Result:")
for row in result:
    print(row)

Again nested loops .

Let me explain everything:

• matrix1 and matrix2 are two matrices defined using nested lists.
• result is initialized as a matrix filled with zeros of the same size as matrix1 and matrix2.
• On line number 13 Three nested loops are used to perform matrix multiplication. The loops iterate through the elements of the matrices and calculate the dot product to find the resulting matrix.
• Again, you know the print part.

These examples demonstrate basic matrix addition and multiplication using Python’s built-in lists, without using NumPy.

Where Matrices are Used in Python:

1. Data Science and Machine Learning:

   • Data representation and linear algebra operations in algorithms like regression, classification, and dimensionality reduction.

2. Image Processing and Computer Vision:

   • Representing images as matrices of pixels and using matrices in operations like convolutions in CNNs.

3. Graph Theory and Network Analysis:

   • Matrices represent connections in graphs and are crucial in algorithms like PageRank.

4. Engineering and Physics:

   • Modeling physical systems, solving differential equations, and finite element analysis.

5. Optimization and Operations Research:

   • Matrices are fundamental in solving optimization problems, especially in linear programming.

6. Financial Analysis and Economics:

   • Portfolio optimization, risk management, and input-output analysis in economics.

7. Game Development:

   • Using matrices for transformations (e.g., translations, rotations) in 2D/3D game development.

Python, especially with libraries like NumPy, SciPy, and Matplotlib, facilitates efficient manipulation and operations with matrices, making it versatile across various fields requiring matrix computations.

Conclusion

I hope this article helped you understand the basics of matrices in Python. 🎉

Thanks very much!
Happy hacking!

by @piyushduggal-source (mr_unchained)

Note: I did not use ChatGPT, kasam se..